6-cubic honeycomb
| 6-cubic honeycomb | |
|---|---|
| (no image) | |
| Type | Regular 6-space honeycomb |
| Family | Hypercube honeycomb |
| Schläfli symbol | {4,3,3,3,3,4} {4,3,3,3,31,1} |
| Coxeter-Dynkin diagrams | |
| 6-face type | {4,3,3,3,3} |
| 5-face type | {4,3,3,3} |
| 4-face type | {4,3,3} |
| Cell type | {4,3} |
| Face type | {4} |
| Face figure | {4,3} (octahedron) |
| Edge figure | 8 {4,3,3} (16-cell) |
| Vertex figure | 64 {4,3,3,3,3} (hexacross) |
| Coxeter group | 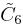 , [4,3,3,3,3,4] , [4,3,3,3,3,4]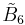 , [4,3,3,3,31,1] , [4,3,3,3,31,1] |
| Dual | self-dual |
| Properties | vertex-transitive, edge-transitive, face-transitive, cell-transitive |
The 6-cube honeycomb or hexeractic honeycomb is the only regular space-filling tessellation (or honeycomb) in Euclidean 6-space.
It is analogous to the square tiling of the plane and to the cubic honeycomb of 3-space.
There are many different Wythoff constructions of this honeycomb. The most symmetric form is regular, with Schläfli symbol {4,3,3,3,3,4}. Another form has two alternating 6-cube facets (like a checkerboard) with Schläfli symbol {4,3,3,3,31,1}. The lowest symmetry Wythoff construction has 64 types of facets around each vertex and a prismatic product Schläfli symbol {∞}6.
See also
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p.296, Table II: Regular honeycombs
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]